(Finally) Getting Better at Teaching Optimization
Sunday, December 22, 2024
In calculus I teach a concept called “optimization,” which, as I tell students, is an application of pretty much everything they’ve ever learned in math class. Not only that, all the problems are “story problems.” It can be a very tough section for students. The irony is that the calculus is not the difficult part. It’s interpreting the situation, sketching it correctly, developing the correct model, integrating constraints into the model, and finally interpreting what the model is telling you.
Teaching this is a headache every year because I have always thought that students basically just need practice with me guiding along the way. I certainly lectured over some sample problems. But it’s impossible to lecture over every possible problem that might come up. There are broad types of problems (volume, shortest path, inscribing under curves, etc.), but simply because a student can understand one volume problem, of a box let’s say, does not mean that they can translate that to a problem involving a cylinder. I basically thought I would cover the basic problem types and let them just do a bunch of problems.
Well, this approach never really “worked.” That is to say that students, on average, almost always struggled with the quiz (some data on that below). Of course, some students would ace it. But far too many (in my mind) good math students would struggle. After the last two years of having strong classes struggle with the quiz the first time AND when they retook it I decided I had to do something different (this was honestly the biggest issue for me - while the retake isn’t a carbon copy of the first version, it’s similar enough that they should improve).
But what to do? How could I teach something that had such a wide range of required skills?
Last year several of us in the math department read a book called How Learning Happens. One of the things it talks about is explicit instruction and how to use it to teach complex topics. Essentially you break the concept into it’s constituent parts and sub-skills, teach the sub-skills explicitly and have students practice, and then build that up until you get to the problems which you ultimately want them to do independently. Seems obvious, but again, the wide range of problems in this concept had me scratching my head – how could I break these down into “smaller” parts?
I realized that every problem required finding a mathematical model and optimizing that function (this is called the target function). Then a student needs to take that target function and either apply calculus using the derivative (again, not the difficult part) or graphing and interpreting the graph. I decided that we would do a handful of problems where I presented the situation and gave them the model. This allowed them to see how the problems would be presented and then how they would solve them with the model. They could focus on interpreting the function, why a constraint equation might be needed and how to use it, and then how to solve it.
Essentially this took the hardest part out of the problems and allowed them to focus on the end stage - optimization the target function.
Why start with this? If the hardest part is the set up, then shouldn’t you spend more time there?
Well, it may be the hardest part, but the end stage of these problems is not necessarily easy. This is especially true if you’ve spent a lot of cognitive energy setting it up. The goal was to teach them how to take the model and the constraint and solve it. Thereby reducing the cognitive energy needed to finish out the problems. (The other problem I failed to mention above is that doing many of these problems is exhausting. The more that we can reduce the mental energy exerted per problem, the more problems they will be able to engage with in a given session. The more problems they engage with – the wider the variety of problems – the better they will get at solving them.) Think of it like this. A basketball player practices layups countless times in practice so that in the game she needn’t worry about the last part of scoring. She can focus on beating the defender to the hoop, not getting the ball in the hoop after she’s done the hard part.
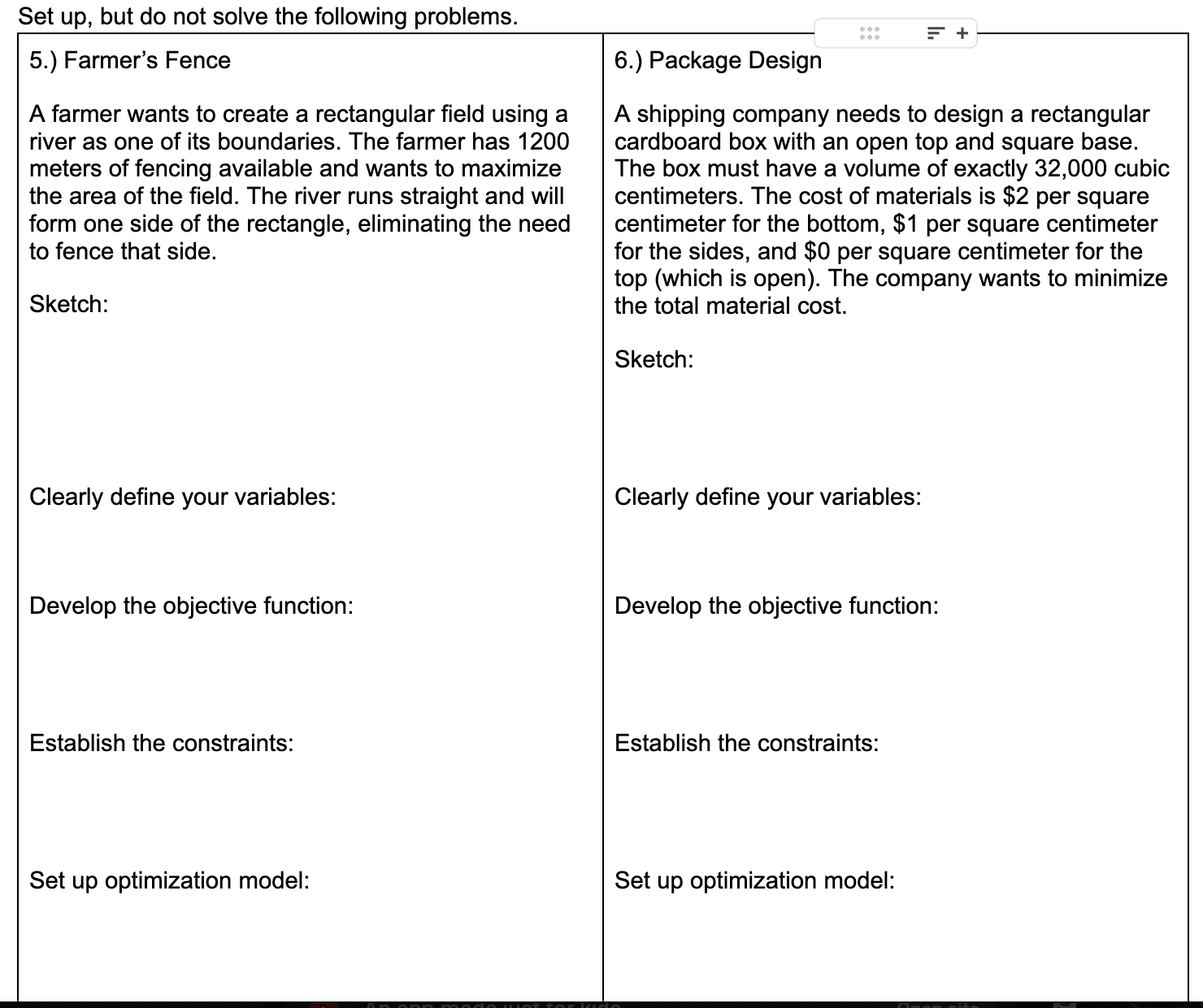
The next phase I took students through was the setup phase. I wanted students to sketch the situation, define variables, identify the target function and the constraint, and set up the model they would optimize. That’s it. No finishing out the problem. We just learned that.
This also allowed me to get students exposed to more problems. Time is a huge factor as each problem can take a relatively large amount of time if you take it from start to finish. It also gave students a framework for approaching the problems. If they could figure out each part of the framework then they had a much greater chance to ultimately solve the problem.
Finally, I brought in the full problems and showed how to take a few problems from start to finish. After that they had plenty of independent work time with me assisting as needed.
There was a lot of guided practice the first couple of days, with me explicitly teaching much more than I have in previous years. It was a classic “I do/we do then you do” approach and the problems seemed to go much better than in previous years as indicated by handling fewer questions during class. This was demonstrated by their assessment scores as well. Here are their mean and median scores as compared to previous years. Remarkably, the averages from previous years are after students had the opportunity to retake the quiz. This year’s scores will certainly go up, if only a small amount, once students have the opportunity to retake them.
2022
- Mean: 17.8
- Median: 18.25
2023
- Mean: 16.5
- Median: 17.5
⠀This year (2024)
- Mean: 17.8
- Median: 19
The overall strength of this class is not notably better than previous years, so I don’t think that explains the improvement. Especially compared to my 22-23 group.
It’s also worth noting what I didn’t do and have done in the past. I did not introduce this concept using any inquiry activities. I used to have students cut squares out of the corners of paper and try to make the open top box with the largest volume. There’s nothing wrong with this activity. It’s kind of fun and introduces the concept in a physical way. I just think it adds minimal value in terms of actually solving the problems.
The takeaway here is that even “problem solving” can be scaffolded. Students can’t solve novel problems until they have plenty of background knowledge required to solve them. We – and I for a long time – often assume students see problems as we (experts) do, but they don’t. When an expert looks at a problem he or she can immediately identify the structure of the problem and how to approach it. Novices (our students) cannot do that. This means that they spend a lot of cognitive energy pursuing approaches that won’t work or aren’t optimal. Providing structure to the problems, explicitly teaching the structure, teaching the concept in chunks allowing exposure to more problems, and finally allowing independent work time with me available seemed to be a fundamentally better approach to teaching optimization.
Here is the note-taking guide that I used this year. The first two pages are what I added this year and the last two pages are basically all I did in previous years.